Statistical Analysis Using Random Forest Algorithm Provides Key Insights into Parachute Energy Modulator System
Download PDF: Statistical Analysis Using Random Forest Algorithm Provides Key Insights into Parachute Energy Modulator System Energy modulators (EM), also known as energy absorbers, are safety-critical components that are used to control shocks and impulses in a load path. EMs are textile devices typically manufactured out of nylon, Kevlar® and other materials, and control loads […]

Energy modulators (EM), also known as energy absorbers, are safety-critical components that are used to control shocks and impulses in a load path. EMs are textile devices typically manufactured out of nylon, Kevlar® and other materials, and control loads by breaking rows of stitches that bind a strong base webbing together as shown in Figure 1. A familiar EM application is a fall-protection harness used by workers to prevent injury from shock loads when the harness arrests a fall. EMs are also widely used in parachute systems to control shock loads experienced during the various stages of parachute system deployment.
Random forest is an innovative algorithm for data classification used in statistics and machine learning. It is an easy to use and highly flexible ensemble learning method. The random forest algorithm is capable of modeling both categorical and continuous data and can handle large datasets, making it applicable in many situations. It also makes it easy to evaluate the relative importance of variables and maintains accuracy even when a dataset has missing values.
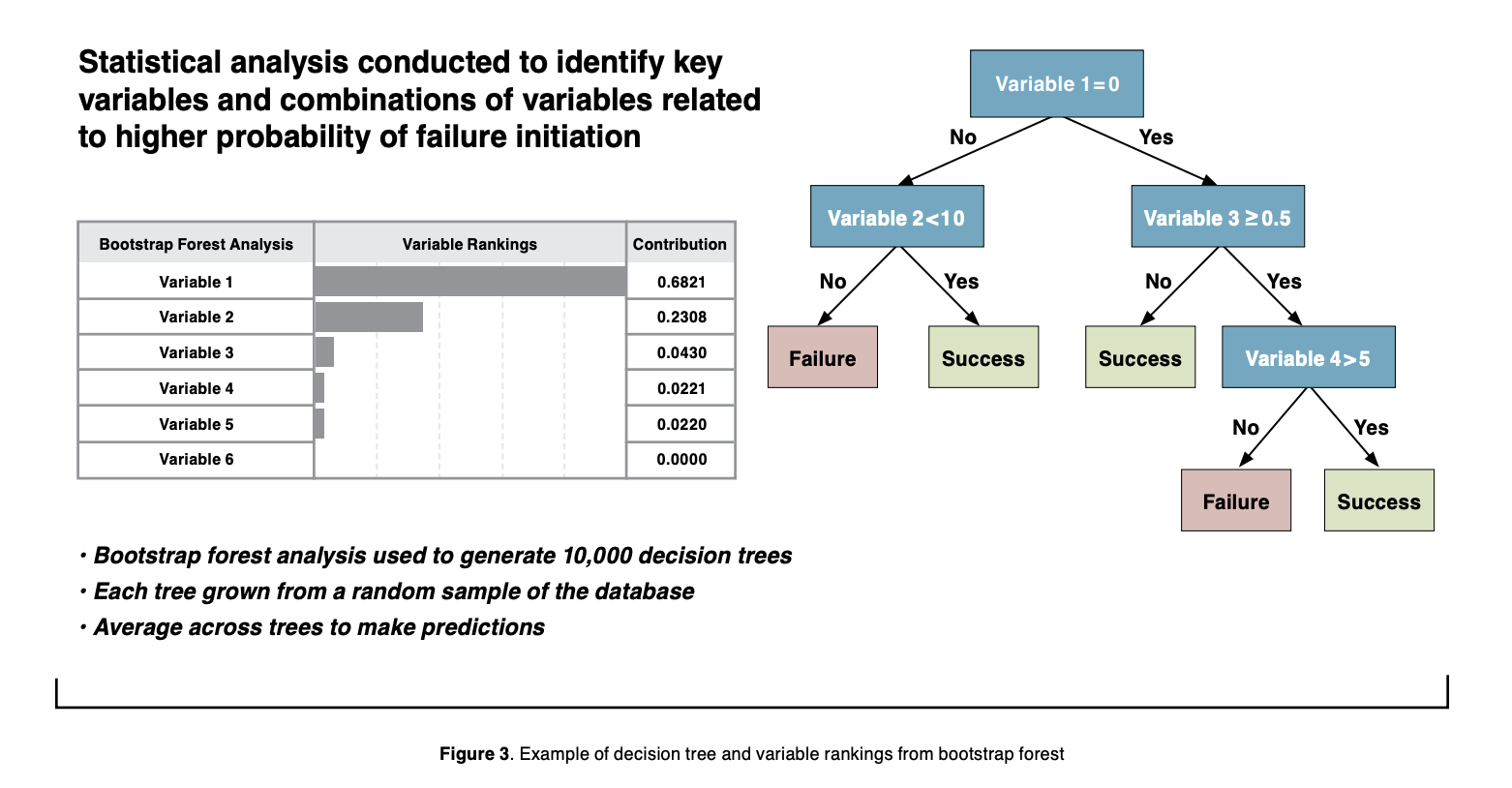
Random forests model the relationship between a response variable and a set of predictor or independent variables by creating a collection of decision trees. Each decision tree is built from a random sample of the data. The individual trees are then combined through methods such as averaging or voting to determine the final prediction (Figure 2). A decision tree is a non-parametric supervised learning algorithm that partitions the data using a series of branching binary decisions. Decision trees inherently identify key features of the data and provide a ranking of the contribution of each feature based on when it becomes relevant. This capability can be used to determine the relative importance of the input variables (Figure 3). Decision trees are useful for exploring relationships but can have poor accuracy unless they are combined into random forests or other tree-based models.
The performance of a random forest can be evaluated using out-of-bag error and cross-validation techniques. Random forests often use random sampling with replacement from the original dataset to create each decision tree. This is also known as bootstrap sampling and forms a bootstrap forest. The data included in the bootstrap sample are referred to as in-the-bag, while the data not selected are out-of-bag. Since the out-of-bag data were not used to generate the decision tree, they can be used as an internal measure of the accuracy of the model. Cross-validation can be used to assess how well the results of a random forest model will generalize to an independent dataset. In this approach, the data are split into a training dataset used to generate the decision trees and build the model and a validation dataset used to evaluate the model’s performance. Evaluating the model on the independent validation dataset provides an estimate of how accurately the model will perform in practice and helps avoid problems such as overfitting or sampling bias. A good model performs well on
both the training data and the validation data.
The complex nature of the EM system made it difficult for the team to identify how various parameters influenced EM behavior. A bootstrap forest analysis was applied to the test dataset and was able to identify five key variables associated with higher probability of damage and/or anomalous behavior. The identified key variables provided a basis for further testing and redesign of the EM system. These results also provided essential insight to the investigation and aided in development of flight rationale for future use cases.
For information, contact Dr. Sara R. Wilson. sara.r.wilson@nasa.gov
What's Your Reaction?



















.jpg?#)